
1, review
The pressure drop of the copper wire is related to its resistance, and its resistance calculation formula:
At 20°C: 17.5 ÷ cross-sectional area (mm 2 ) = resistance per kilometer (Ω)
At 75°C: 21.7 ÷ cross-sectional area (mm 2 ) = resistance per kilometer (Ω)
The pressure drop calculation formula (by Ohm's law): V=R×A
The line loss is related to the voltage drop and current used.
Its line loss calculation formula: P=V×A
P-Line Loss Power (Watts) V-Voltage Drops (Volts) A-Line Current (Amps)
2, copper core power line current calculation method
1mm2 copper power line safe carrying capacity - 17A.
1.5mm2 copper power line safe carrying capacity - 21A.
2.5mm2 copper power line safe carrying capacity -28A.
Safe Current Carrying Capacity of 4mm2 Copper Power Cable - 35A
6mm2 copper power line safe current capacity - 48A
10mm2 copper power line safe carrying capacity - 65A.
16mm2 copper power line safe current capacity - 91A
25 mm2 copper power line safe carrying capacity - 120A.
The single-phase load is 4.5 A per kilowatt (COS & = 1). After the current is calculated, the conductor is selected.
3. Current comparison method between copper core and aluminum core wire
2.5 mm 2 copper wire is equal to 4 mm 2 aluminum wire
4mm2 copper wire is equal to 6mm2 aluminum wire
6mm2 copper wire is equal to 10mm2 aluminum wire
<10 square millimeters or less multiplied by five>
That is: 2.5 mm2 copper wire = <4 mm2 aluminum wire x 5> 20 amps = 4400 kW;
4 square millimeter copper core wire = <6 square millimeter aluminum core wire x 5> 30 ampere = 6600 kilowatts;
6 square millimeter copper core wire = <10 square millimeter aluminum core wire x 5> 50 amperes = 11000 kilowatts
The soil method is one square 1KW of copper core wire and 2 squares 1KW of aluminum core. The unit is square millimeter.
Is the cross-sectional area (mm 2 )
The current capacity of the cable varies depending on the copper/aluminum core. You can use 2.5 (mm2) for the copper core. Its standard:
0.75/1.0/1.5/2.5/4/6/10/16/25/35/50/70/95/120/150/185/240/300/400...
There are non-national standards such as: 2.0
Aluminum core 1 square maximum current carrying capacity 9A, copper core 1 square maximum current carrying capacity 13.5A
Multiply the number by 9.5 and increase the number by 9.
Thirty-five to three-by-five, and both teams lose five points.
The conditions are changed and converted, and the high temperature 10% copper upgrade.
The number of pipes worn was 234, and the full load was 876.
1, "By 5: multiplying by 9 and going up one minus sign" is:
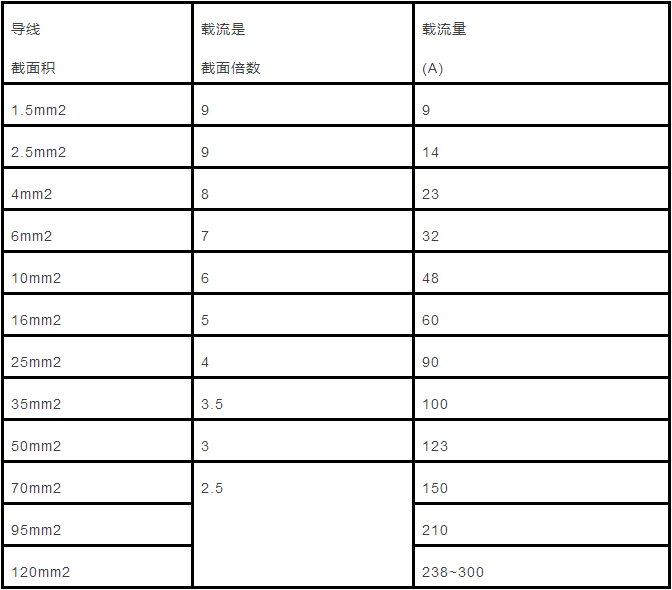
All kinds of cross-section aluminum core insulated wire of 2.5mm' or below have a current carrying capacity of about 9 times the number of sections. Such as 2.5mm' wire, the current capacity of 2.5 × 9 = 22.5 (A). The multiple of the current carrying capacity and the number of cross-sections of the conductors from 4 mm′ and above is the row along the line number, and the multiple is successively reduced by l, that is, 4×8, 6×7, 10×6, 16×5, and 25×4.
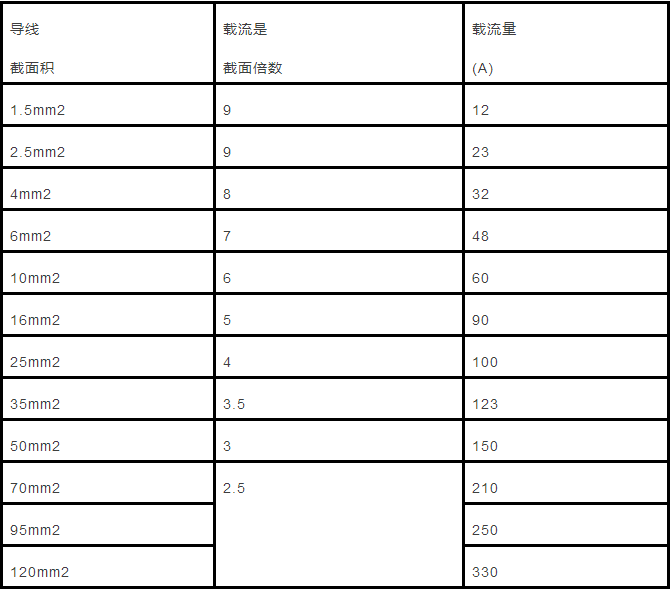
2, "35 by 3.5, both groups minus 5," said:
The 35mm†wire carrying capacity is 3.5 times the number of sections, that is, 35×3.5=122.5(A). From 50mm′ and above, the multiple relationship between the current carrying capacity and the number of sections becomes The two wire numbers are grouped, and the multiple is reduced by 0.5. That is, the carrying capacity of the 50 and 70mm' wire is 3 times the cross-sectional area; the 95, 120mm wire carrying capacity is 2.5 times the cross-sectional area. And so on.
3. "Conditions are subject to change, high temperature 10% copper upgrade".
The above-mentioned mouthpiece is made of an aluminum core insulated wire and an open coating under the condition of an ambient temperature of 25°C. If the aluminum core insulation wire is deposited in an area where the ambient temperature is higher than 25°C for a long time, the wire carrying capacity can be calculated according to the above formula, and then it can be used for 10%. When the aluminum wire is used instead of the aluminum wire, the copper core wire is used. Its ampacity is slightly larger than that of the aluminum wire of the same specification. The ampacity method can be used to calculate the ampacity of a line number larger than that of the aluminum wire. For example, the current carrying capacity of 16mm' copper wire can be calculated as 25mm2 aluminum wire.
2.5mm2 copper power line safe carrying capacity -28A.
4mm2 copper power line safe carrying capacity - 35A.
6mm2 copper power line safe carrying capacity - 48A.
10mm2 copper power line safe carrying capacity - 65A.
16mm2 copper power line safe carrying capacity - 91A.
25 mm2 copper power line safe carrying capacity - 120A.
If it is an aluminum wire, the wire diameter should be 1.5-2 times that of the copper wire.
If the copper current is less than 28A, it is safe to take 10A per square millimeter.
If the copper current is greater than 120A, take 5A per square millimeter.
The current through which the cross-sectional area of ​​the wire can normally pass can be selected according to the total number of currents that it needs to conduct. Generally, it can be determined as follows:
Ten in five, one in two,
The 2553 4 community,
Pick up five and a half and half
Copper upgrade calculation.
Explain to you:
That is, aluminum wire below 10 squares can be multiplied by 5 in square millimeters. If it is copper wire, it should be raised to a file, such as 2.5 square copper wire, and it should be calculated in 4 squares. More than 100 times are cross-sectional area times. Multiply it by 2, 25 or less squares, multiply it by more than thirty-five squares by 3, pick it up, and multiply by 95 squares by 2.5. It's worth remembering a few sentences.
Five to five, one hundred twenty-five, twenty-five, thirty-five, four or three circles seventy, ninety-five and two hundred and fifty-fifths half-finished lines plus half, copper upgrades are counted through the pipe, and the high temperature is eight or ten percent off.
1. The “Ten-Five†guideline section is 10 square millimeters and below, and the safety current per 1 square millimeter is 5 amps.
2. The guideline of "One-hundred-second" guideline is more than 100 square millimeters, and the safety current per 1 square millimeter is 2 ampere.
3. The “25, 35, and 43†sector guideline is 25mm2 and 16mm2, and the safety current per 1mm2 is 4A. The conductor cross-section is 35 mm2 and 50 mm2, and the safety current per 1 mm2 is 3 amps.
4. The “70, 95×2†guideline section is 70 square millimeters and 95 square millimeters, and the safety current per 1 square millimeter is 2.5 amps.
“Bare wire plus half, copper wire upgrade calculation†refers to the bare wire of the same cross section. The safe current can be calculated by multiplying the insulated wire by 1.5 times. The same section of the copper conductor is calculated according to the grade of the aluminum conductor, and the safety electric p=ui42000/220=191A pure resistive element. 150 square feet of cable is recommended.
1 square plastic insulated wire safe current carrying value:
The Ming Line - 17 An,
Wearing steel pipes: two ─ 12 amps, three ─ 11 amps, four ─ 10 amps,
Wear plastic pipe: two - 10 A, three - 10 A, four - 9 A.
Sheath line: two cores - 13A, three cores and four cores - 9.6A.
Rubber Insulated Wire; Bright Line - 18A, Through Steel Pipe: Two - 13A, Three - 12A, Four - 11A
Explanation: It can only be used as an estimate, not very accurate.
In addition, if you press the room to remember copper wire below 6mm2, it is safe to use less than 10A per square current. From this perspective, you can choose 1.5 square copper wire or 2.5 square aluminum wire.
Within 10 meters, the wire current density is 6A/mm2, 10-50 meters, 3A/mm2, 50-200 meters, 2A/mm2, 500 meters or more is less than 1A/mm2. From this point of view, if you are not far away, you can choose 4 square copper wire or 6 square aluminum wire.
If it is really 150 meters from the power supply (not to mention high-rise), we must use 4 square copper wire.
The impedance of a wire is proportional to its length and inversely proportional to its wire diameter. When using the power supply, pay special attention to the wire and wire diameter of the input and output wires. To prevent the current from overheating the auxiliaries lead to accidents.
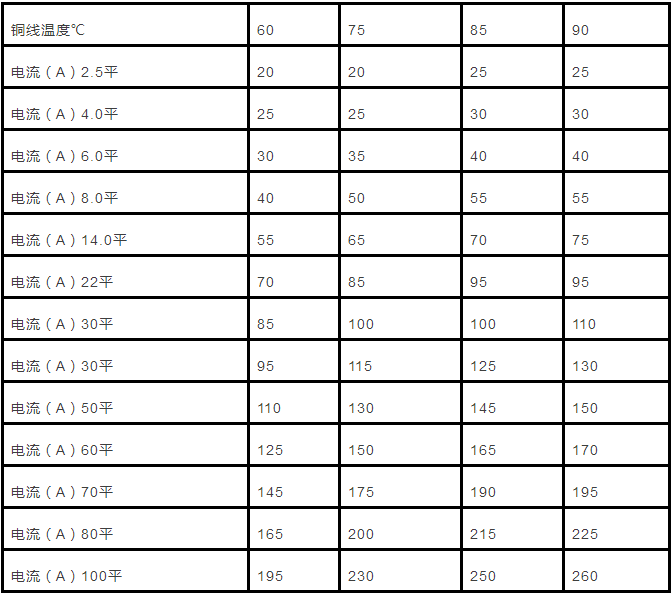
Below is a table of wire diameters and maximum currents that the copper wire can withstand at different temperatures.
Wire diameter (approximate) (mm2)
4, wire diameter calculation
The wire diameter is generally calculated according to the following formula:
Copper wire: S = IL / 54.4*U`
Aluminum wire: S= IL / 34*U`
In the formula:
I - The maximum current through the wire (A)
L - length of wire (M)
U`——Power Supply Drop (V)
S - cross-sectional area of ​​the wire (MM2)
Explanation:
1. The voltage drop of U` can be considered by selecting the power supply voltage rating for the system power supply used by the entire system (such as the detector).
2. Calculate the cross-sectional area upwards. Estimate the current carrying capacity of insulated wire.
★Multiple relationship between current carrying capacity and cross section of aluminum core insulated wire (25 degrees)
★Multiple relationship between current carrying capacity and cross section of copper core insulated wire (25 degrees)
5, carrying capacity
Estimates:
Multiply the number by 9.5 and increase the number by 9.
Thirty-five to three-by-five, and both teams lose five points.
The conditions are changed and converted, and the high temperature 10% copper upgrade.
The number of pipes worn was 234, and the full load was 876.
Explanation:
In this section, the current-carrying capacity (safety current) of various types of insulated wires (rubber and plastic insulated wires) is not directly indicated, but is expressed by “multiply the cross-section by a certain factorâ€, which is calculated by mental arithmetic. It can be seen from Table 53 that the multiple decreases with the increase of the cross section.
1, "By 5: multiplying by 9 and going up one minus sign" is:
All kinds of cross-section aluminum core insulated wire of 2.5mm' or below have a current carrying capacity of about 9 times the number of sections. Such as 2.5mm' wire, the current capacity of 2.5 × 9 = 22.5 (A). The multiple of the current carrying capacity and the number of cross-sections of the conductors from 4 mm′ and above is the row along the line number, and the multiple is successively reduced by l, that is, 4×8, 6×7, 10×6, 16×5, and 25×4.
2. "Thirty-five by three-fifth, both groups minus five points" is:
The 35mm†wire carrying capacity is 3.5 times the number of sections, that is, 35×3.5=122.5(A). From 50mm′ and above, the multiple relationship between the current carrying capacity and the number of sections becomes The two wire numbers are grouped, and the multiple is reduced by 0.5. That is, the carrying capacity of the 50 and 70mm' wire is 3 times the cross-sectional area; the 95, 120mm wire carrying capacity is 2.5 times the cross-sectional area. And so on.
The above-mentioned mouthpiece is made of an aluminum core insulated wire and an open coating under the condition of an ambient temperature of 25°C. If the aluminum core insulation wire is deposited in an area where the ambient temperature is higher than 25°C for a long time, the wire carrying capacity can be calculated according to the above formula, and then it can be used for 10%. When the aluminum wire is used instead of the aluminum wire, the copper core wire is used. Its ampacity is slightly larger than that of the aluminum wire of the same specification. The ampacity method can be used to calculate the ampacity of a line number larger than that of the aluminum wire. Such as 16mm' copper current carrying capacity, according to 25mm2 aluminum line, the greater the cross-sectional area, the smaller the resistance, the greater the current through the same voltage.
Household electrical wiring is generally calculated using the empirical formula in the home circuit system layout method. The choice of conductors is copper conductors. The empirical formula is: conductor cross section (in square millimeters) ≈I/4(A).
The rated current capacity of a copper conductor of about 1 mm2 is ≈4A, and the rated current capacity of a copper conductor of 2.5 mm2 is about 10 amps.
Actually, the current-carrying capacity of the wire mainly depends on the heat-dissipation condition of the wire and the importance of the location of the wire.
The heat-dissipating conditions of the overhead laying wires are better, and the heat dissipation conditions for the closed concealed conductors such as pipes and buried walls are worse; multiple wires have worse heat dissipation conditions than a single wire, and the more wires in one tube, the poorer the heat dissipation. Wires of the same size can have larger download flow under good heat dissipation conditions, and smaller download conditions when heat dissipation conditions are poor.
The location of cabling is very important, the safety requirements are high, and the ampacity is small. It is not a very important place where the ampacity is greater. The above stated home wiring wire carrying capacity is very small.
The stringent requirement is to multiply the conductor cross-sectional area by 4 as the current carrying capacity. With a small current carrying capacity, the wires are much more expensive. In order to reduce costs and ensure safety, many home improvement products use wire cross-sectional area multiplied by 5 or 6 times to increase the current carrying capacity of the wire when it is not closed wiring.
This is also the maximum current-carrying capacity of home wiring, and once again, there is no guarantee that home appliances can be safely used. In the case of industrial power, the current-carrying capacity can be multiplied by approximately 9 times the cross-sectional area of ​​the conductor.
Using the home wiring experience formula to see the 2.5 square copper conductor wire carrying capacity is 2.5*4 is right, 2.5*5 can also be useful 2.5*6. However, 2.5*9 or even 2.5*10 can be used in places with good heat dissipation conditions such as factories.
In short, the same conductor has different current carrying capacity under different conditions and different requirements.
The following gives a guideline to allow you to refer to the long-term allowable ampacity meter. Its ampacity is also conditional and is the largest.
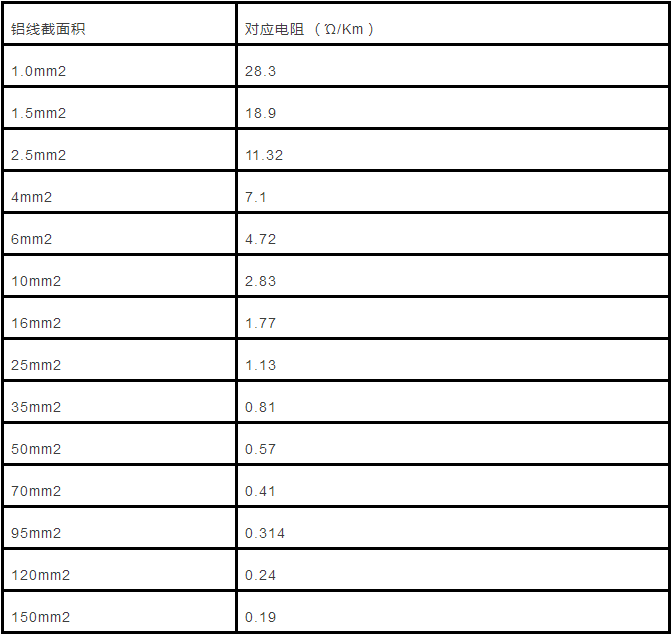
6, copper and aluminum wire resistance per kilometer
1. Nominal sectional area / (Copper wire)

2. Nominal sectional area / (Aluminum core wire)
Resistance formula:
Voltage Drop = 2X Resistance X Device Total Current - AC Voltage = Device Supply Voltage
R=p*l/s
P- resistivity look-up table
L—resistance length;
s—The cross-sectional area of ​​the resistor perpendicular to the current
The two resistors R increase in series and become 2R, meaning that the length is increased by 1 time, the resistance value is increased by 1 time, and the resistance is proportional to the length.
Two resistors R are connected in parallel, 1/2R, the cross-sectional area is increased by 1 times, the resistance value becomes 1/2, and the resistance is inversely proportional to the cross-sectional area.
therefore:
R=pl/S. p=RS/l
The wire is a water pipe. The current is the small fish in the pipe. When the pipe is long, the fish feels very difficult to resist from the end to the end. Of course, the thinner the pipe, the smaller the section is, the more it moves to the other end. difficult. The resistivity is a constant of the resistance of water to fish. No matter how long or thin your tube is, the resistance of water to fish (electron) is the same as the tube of water. The resistivity of copper is 0.0175 and the resistivity of aluminum is 0.026. From the aspect of current carrying capacity, 4 square copper is equivalent to aluminum wire 4*0.026/0.0175=4*1.485=5.94 square.
However, due to the poor heat resistance of aluminum than copper, the available current of 4 square copper wire can exceed 6 square aluminum wires.
10 square two-core cable, the temperature allows 20 amperes for 75A, the voltage drop is 4.67MV / m under 220V voltage can be driven within 16.5KW electrical cross-section 1 square millimeters length of 1 m copper wire resistance at 20 degrees Celsius 0.018 ohms, R=P*L/S (P-resistance coefficient, L length, meters, and S-square cross-section, mm), resistance is 0.72 ohms.
The line loss calculation at 220V is:
P=I2R(p loss power W, i device current, r cable resistance)
Set the device current to 50A when working, then the loss power is 50*2*0.72=72W.
The resistivity should be
p=0.0175 Euro.mm^2/m = 1.75*10^-8 Euro.m
L=6000mm=6m, S=6mm^2
R=pL/S=0.0175*6/6=0.0175 Euro
R=PL/S
R is the resistance (unit is Ω), P is the resistivity of this kind of material (the resistivity of copper is 0.0175), L is the length of the conductor in the current direction (unit is m), S is the direction of the conductor perpendicular to the current Cross-sectional area (in square meters).
The weight is calculated using M=PV, M is the weight (in kilograms), P is the density (copper density=8.9 x 103 kilograms/cubic meter), and V is the volume (in cubic meters).
7, for example
If 500W power uses many squared cables? ? What is this calculation formula?
It depends on whether you use three-phase or single-phase.
Single-phase press P=UI
Three-phase press P=1.732*UI
Suppose you are single-phase: P=UI I=P/U=500/220=2.27
Suppose you are three phases: P=1.732UI I=P/1.732U=500/1.732*380=0.75A
Voltage drop = current * wire resistance
Wire resistance = (wire length * resistivity) / cross-sectional area of ​​wire
Current = electric power / electric voltage
The resistivity of copper = 1.75*10-8 power.
The 1.5 square copper wire is a 1.5mm2 cross-sectional area copper wire, so the 2000m long copper wire resistance (normal temperature) is:
(2000m*1.75*10-8 power.m)/1.5*10-6 power m2=23.33 ohms
So if you pass a current of 1A on the wire, the pressure drop is 23.3V. That is, the voltage drop per square meter is 0.0024mv.
If you use electrical appliances with a rated power of 1 kilowatt and a working voltage of 220 volts, then with such a wire, the voltage drop is: 71.5 volts (approximately one-third of the power is wasted on the wire) If you take it 100 watts of power, then the pressure drop is: 10.1V (basically can be ignored, does not affect the normal operation of electrical appliances)
Therefore, it is recommended that the power should not exceed 200W. If it exceeds 200W, the actual voltage on your electrical appliance will be less than 200V.
Calculated in 3 steps, indicating the load, taking the motor as the load.
1, the length of wire: L = 400 meters,
Motor power: 15kw+12kw+18kw=45KW,
Current: I≈90A, copper cross section: S=25 square,
Copper wire resistivity: Ï=0.0172
Find the line resistance at 400 meters (single line):
R=Ï×(L/S)=0.0172×(400/25)≈0.275(Ω)
Find the distance from the voltage drop of 400 meters (single line): U=RI=0.275×90≈25(V)
The segment voltage is:
380-25×2 (double line)=330(V)
2, the length of wire: L = 600-400 = 200 meters,
Motor power: 12kw+18kw=30KW, I≈60A
Find the line resistance at 200 meters (single line):
R=Ï×(L/S)=0.0172×(200/25)≈0.138(Ω)
Find a voltage drop of 200 meters (single line):
U=RI=0.138×60≈8(V)
The segment voltage is:
380-(25+8)×2=314(V)
3, the length of wire: L = 700-600-400 = 100 meters,
Motor power: 18KW,
I≈36A
Find the line resistance at 100 meters (single line):
R=Ï×(L/S)=0.0172×(100/25)≈0.069(Ω)
Find a voltage drop of 100 meters (single line):
U=RI=0.069×36≈2.5(V)
The terminal voltage is:
380-(25+8+2.5)×2=309(V)
Example: If 4 square (mm) copper wire is used, the length of the wire is 200m (three-phase four-wire). So what is the power consumption of the 30th line? How much is the 6 square (mm) line?
1 square millimeter equals 1/1000000 square meters
(1 square millimeter=0.01 square centimeter=0.0001 square decimeter=0.0000 01 square meters, 1 millimeter=1/1000 meters
1 square millimeter = 1/(1000*1000) square meters)
Object resistance formula:
R=ÏL/S
In the formula:
R is the resistance of the object (ohms);
Ï is the resistivity of the material in ohms (Ω. mm2/m).
L is the length in meters (m)
S is the sectional area in square meters (mm2)
Ohm's Law (I=U/R)
The voltage drop on the wire is equal to the product of the current in the wire and the wire resistance (U=I*R)
Power calculation formula P = U2/R (U stands for voltage, R stands for resistance)
The resistivity of the pure silver wire at 0°C is 0.016 Ω.mm2/m (ohmmeter), the resistivity of the pure copper wire at 0°C is 0.0175 Ω.mm2/m (ohmmeter), and the temperature coefficient of resistance is 0.00393/°C. . The resistivity of pure aluminum wire at 0°C is 0.0283 Ω.mm2/m (ohmmeter).
Ï=Ïo(1+a*t)
In the formula
Ï - resistivity at t degrees Celsius
Ρo - resistivity at 0°C
T——temperature
The resistivity of the pure copper wire at 21°C = 0.0175(1+0.00393*21)=0.0189 Ω.mm2/m) R=0.0175X200/4=0.875 ohms
On the 30th of the power consumption, if the voltage is 220V, then the first required power P = U2/R = 2202/0.875 = 55.314W
(This state is that the electric wire directly constitutes a loop, that is to say it does not receive any household appliances. If it is really such a short-circuit conference, it will trip!)
55.314X30X24÷1000=39.826 degrees (1 kWh = 1 kWh)
Voltage loss = ∑(P*L)/(C*S)
P: total circuit power (KW) L: distance from the power supply to the load (m) C: material coefficient (at 380V, copper 77, aluminum 46.3; 220V, copper take 12.8, aluminum take 7.75) S: conductor cross-sectional area ( Mm)
8, different temperature resistivity
Resistance of several metal conductors at 20°C
(1) Silver 1.65 (Europe) × 10-8 (M)
(2) Copper 1.75 × 10-8
(3) Aluminum 2.83 × 10-8
(4) Tungsten 5.48 × 10-8
(5) Iron 9.78 × 10-8
(6) Platinum 2.22 × 10-7
(7) Manganese copper 4.4 × 10-7
(8) Mercury 9.6 × 10-7
(9) Kang Copper 5.0 × 10-7
(10) Nickel-chromium alloy 1.0 × 10-6
(11) Iron-chromium alloy 1.4 × 10-6
(12) Inconel 1.6 × 10-6
(13) Graphite (8 to 13) 10-6
Gear Sensor has been widely used in the automotive and industrial field, which is important to the measurement of velocity, angel, angular velocity, direction of rotation.
Gear Sensor,Custom Gear Sensor,Gear Sensor 3 Pins,Good Gear Sensor
Yuheng Optics Co., Ltd.(Changchun) , https://www.yuhengcoder.com